Distributional Reinforcement Learning with Dual Expectile-Quantile Regression
Sami Jullien, Romain Deffayet, Jean-Michel Renders, Paul Groth, Maarten de Rijke
ArXiv'24
Paper | Code
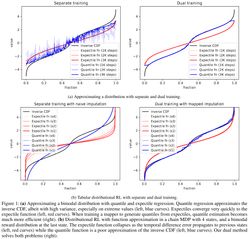
Distributional reinforcement learning (RL) has proven useful in multiple benchmarks as it enables approximating the full distribution of returns and makes a better use of environment samples. The commonly used quantile regression approach to distributional RL -- based on asymmetric L1 losses -- provides a flexible and effective way of learning arbitrary return distributions. In practice, it is often improved by using a more efficient, hybrid asymmetric L1-L2 Huber loss for quantile regression. However, by doing so, distributional estimation guarantees vanish, and we empirically observe that the estimated distribution rapidly collapses to its mean. Indeed, asymmetric L2 losses, corresponding to expectile regression, cannot be readily used for distributional temporal difference learning. Motivated by the efficiency of L2-based learning, we propose to jointly learn expectiles and quantiles of the return distribution in a way that allows efficient learning while keeping an estimate of the full distribution of returns. We prove that our approach approximately learns the correct return distribution, and we benchmark a practical implementation on a toy example and at scale. On the Atari benchmark, our approach matches the performance of the Huber-based IQN-1 baseline after 200M training frames but avoids distributional collapse and keeps estimates of the full distribution of returns.